寒假训练补题记录
XCPC 2021 Happy Winter Vacation #1
E. 护花行动(差分、单调队列)
https://acm.ecnu.edu.cn/contest/361/problem/E/
补的时候感觉比想象中巧妙很多,特别是差分的部分,花了很长时间才理解(甚至补完了觉得也没完全理解)。
从朴素的角度看,如果我想知道能放下几个$x\times y$的矩阵,那我就枚举每个格子,把当前格子作为右下角,看看能不能放的下这个$x\times y$的矩阵。换言之,我只要知道“对于每个格子,我以这个格子为右下角,再枚举宽$a$,如果放一个宽为$a$的矩阵,它的高$b$最多为多少”,如果高为$b$,那我就令$ans[a][b]++$。求出$ans$数组之后,输入为$x\times y$时的答案就是$\sum\limits_{z>=y} ans[x][z]$,这个求和可以直接做一次前缀和来预处理出来,所以不算在复杂度里。
问题在于怎么求解$ans$数组,直接暴力是$O(n^3)$,但是可以发现,随着$a$的增大,$b$是单调减少的,也就是说很可能会存在很多段连续的$a$,它们对应的$b$大小是相同的,那么我就用差分数组+前缀和的方法,$O(1)$实现$ans[L][b]$到$ans[R][b]$这段区间的修改。把每个$b$记录在单调递增队列里,那么整体复杂度就变成了$O(n^2k)$,其中$k$是每个状态下单调队列的平均长度。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 5;
struct S {
int l, r, h;
S(){}
S(int L, int R, int H):l(L), r(R), h(H){}
}st[N];
int top;
int n, m, k, a[N][N], ans[N][N];
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = 1;
}
}
for (int i = 1; i <= k; i++) {
int x, y; scanf("%d %d", &x, &y);
a[x][y] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j]) a[i][j] += a[i - 1][j];
}
}
for (int i = 1; i <= n; i++) {
int tp = 0;
for (int j = 1; j <= m; j++) {
if (!tp || a[i][j] > st[tp].h) {
st[++tp] = S(j, j, a[i][j]);
} else {
while(tp && a[i][j] <= st[tp].h) tp--;
tp++;
st[tp] = S(st[tp].l, j, a[i][j]);
}
for (int k1 = 1; k1 <= tp; k1++) {
int R = j - st[k1].l + 1;
int L = j - st[k1].r + 1;
ans[L][st[k1].h]++;
ans[R + 1][st[k1].h]--;
}
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
ans[i][j] += ans[i - 1][j];
}
}
for (int i = 1; i <= m; i++) {
for (int j = n - 1; j >= 1; j--) {
ans[i][j] += ans[i][j + 1];
}
}
int T; cin >> T;
for (int i = 1; i <= T; i++) {
int x, y; scanf("%d %d", &x, &y);
printf("%d\n", ans[y][x]);
}
return 0;
}
虽然直觉上这个复杂度已经比较优秀而且可以通过这道题了,但是好像还是有退化成$O(n^3)$的可能性。所以其实是有办法优化到$O(n^2)$的,但是计算方法会相对来说更抽象一点。
我们不能在每一列都对$ans$数组进行更新,而是只在某一段区间在单调队列中弹出时更新$ans$。但是更新的时候要注意不能出现重复的情况,比如说下面这个情况,第二列高度大于第三列,此时第二列出列时,只能计算黄色部分高度,因为低于黄色高度的部分会在之后绿色部分出列时计算,如果都计算的话就会出现重复,同样用差分方法计算的话就是在出列时
ans[j - st[tp - 1].r - 1][max(a[i][j], st[tp - 1].h) + 1]++;
ans[j - st[tp - 1].r - 1][st[tp].h + 1]--;
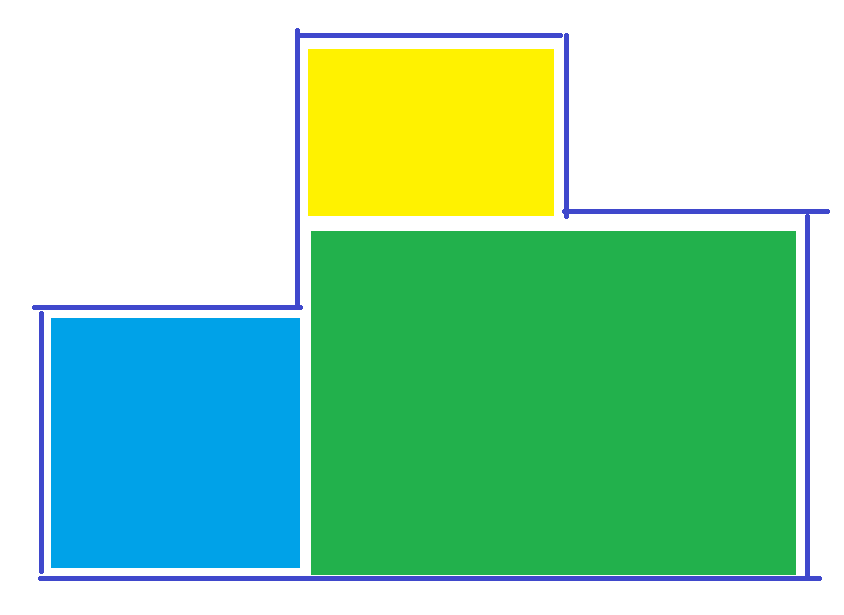
同时这里$ans$又和第一种做法的$ans$不太一样,因为这里只记录了宽度最大的那个矩阵,所以要做两次前缀和。为啥是两次呢,比如有一个$6\times 6$的矩形,那就可以有两个$5\times 6$的,三个$4\times 6$的,四个$3\times 6$,五个$2\times 6$,六个$1\times 6$的。做两次前缀和恰好可以得到这个结果。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 5;
struct S {
int l, r, h;
S(){}
S(int L, int R, int H):l(L), r(R), h(H){}
}st[N];
int top;
int n, m, k, a[N][N], ans[N][N];
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = 1;
}
}
for (int i = 1; i <= k; i++) {
int x, y; scanf("%d %d", &x, &y);
a[x][y] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j]) a[i][j] += a[i - 1][j];
}
}
for (int i = 1; i <= n; i++) {
int tp = 0;
for (int j = 1; j <= m + 1; j++) {
if (!tp || a[i][j] > st[tp].h) {
st[++tp] = S(j, j, a[i][j]);
} else {
while(tp && a[i][j] < st[tp].h) {
ans[j - st[tp - 1].r - 1][max(a[i][j], st[tp - 1].h) + 1]++;
ans[j - st[tp - 1].r - 1][st[tp].h + 1]--;
tp--;
}
while(tp && a[i][j] == st[tp].h) tp--;
tp++;
st[tp] = S(st[tp].l, j, a[i][j]);
}
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
ans[i][j] += ans[i][j - 1];
}
}
for (int j = 1; j <= n; j++) {
for (int i = m - 1; i >= 1; i--) {
ans[i][j] += ans[i + 1][j];
}
for (int i = m - 1; i >= 1; i--) {
ans[i][j] += ans[i + 1][j];
}
}
int T; cin >> T;
for (int i = 1; i <= T; i++) {
int x, y; scanf("%d %d", &x, &y);
printf("%d\n", ans[y][x]);
}
return 0;
}
XCPC 2021 Happy Winter Vacation #3
F. 树上游戏
https://acm.ecnu.edu.cn/contest/363/problem/F/
第一步也是最重要的一步转化是
第二步把所有大于$x$的数视作1,所有小于$x$的数视作0,或者说用0表示较小的那部分数,用1表示较大的那部分数。
第三步用$F[i]$表示走到$i$这个点时选的数是0还是1,根据博弈论知识可以知道
接着开始往叶子结点里填0/1,用$f[x][y][0/1]$表示$x$这棵子树内,有$y$个0,且$F[x]=0/1$的方案数(这里的方案数指的是0/1填法的方案数)。这个dp是一个理论上非常基础但是确实做的比较少的树上背包问题。。类似南京的M题,可以$O(n^2)$解决。
最后$f[1][i][1]$表示填了$i$个0且最后能选到一个大于等于$i$的数的方案数,0和1内部顺序无所谓所以直接乘上排列数$fac[i]$和$fac[m-i]$就有$P(ans >= i) = f[1][i][1]\times fac[i] \times fac[m-i]$
所以其实是用填0/1的方案数一一对应到了某一种填1~m的方案数。而转化成0/1则保证了状态数的有限。
实在是太妙了。
#include <bits/stdc++.h>
#define debug(x) cerr << #x << " = " << x << ' '
#define debugl(x) cerr << #x << " = " << x << '\n'
using namespace std;
typedef long long ll;
const int N = 5e3 + 5, MOD = 1e9 + 7;
inline int add(int a, int b){return a + b >= MOD ? a + b - MOD: a + b;}
inline int sub(int a, int b){return a - b < 0 ? a - b + MOD : a - b;}
inline int mul(int a, int b){return 1LL * a * b % MOD;}
vector<int> G[N];
int n, dp[N][N][2], tmp[N][2], ans, fac[N];
int dfs(int x, int ff, int turn) {
int o = 0, p;
for (auto y : G[x]) {
if (y == ff) continue;
p = dfs(y, x, turn ^ 1);
if (!o) {
o = p;
memcpy(dp[x], dp[y], sizeof(dp[x]));
continue;
}
memset(tmp, 0, sizeof(tmp));
for (int i = 0; i <= o; i++) {
for (int j = 0 ; j <= p; j++) {
int tot = mul(add(dp[x][i][0], dp[x][i][1]), add(dp[y][j][0], dp[y][j][1]));
int t = mul(dp[x][i][turn ^ 1], dp[y][j][turn ^ 1]);
tmp[i + j][turn ^ 1] = add(tmp[i + j][turn ^ 1], t);
tmp[i + j][turn] = add(tmp[i + j][turn], sub(tot, t));
}
}
memcpy(dp[x], tmp, sizeof(tmp));
o += p;
}
if (!o) {
dp[x][0][0] = dp[x][1][1] = 1;
o = 1;
}
return o;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n - 1; i++) {
int u, v; scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
int m = dfs(1, -1, 1);
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = mul(fac[i - 1], i);
for (int i = 1; i <= m; i++) {
ans = add(ans, mul(dp[1][i][1], mul(fac[i], fac[m - i])));
}
cout << ans;
return 0;
}